1. 摘要
2. 低温超导现象
3. 伦敦唯象理论
4. 金兹堡-朗道理论
5. 低温超导的BCS理论
6. 总结

摘要

低温下由于量子效应的涌现,会产生一些非经典的现象,特别是低温超导.如何理解低温超导形成的机制,实际上经历了从唯象到具象,从宏观到微观的探索过程,直到BCS理论的建立才完全解释了低温超导的形成之谜.

低温超导现象

低温超导顾名思义就是指极低温下材料的直流电阻消失所呈现的超导电性.金属低温超导电性的发现打破了人们以往的认识,过去人们知道金属的电导率随着温度的降低而减小,而在极低温下的金属的电导率应该会趋于零,即电阻趋于无穷大.然而1908年Onnes实验发现汞金属在附近电阻突然降为零,即在下汞金属进入了一个新的物态也就是超导态,呈现超导电性^[1][2]. 而为超导的转变温度或临界温度,即表示材料温度满足时出现超导态.后续的实验又发现了更多金属的低温超导现象^[2][3].

Onnes后续的实验还发现当金属温度时,若金属中的电流超过某个临界值后,或者外加磁场的达到某个临界值后,金属的电阻会突然出现的,即超导态被破环转变正常态.这里的为确定温度下的临界电流与临界磁场.对于临界临界磁场,其经验公式为:

这里是指的临界磁场.关于临界电流引起的超导态破坏则可以考虑是由于电流所产生的磁场所引起的超导态破坏,且临界电流产生的磁场在材料表面产生的磁场等于临界磁场.所以有,同样表示时的临界电流.超导电性是超导体最为重要的特征之一.

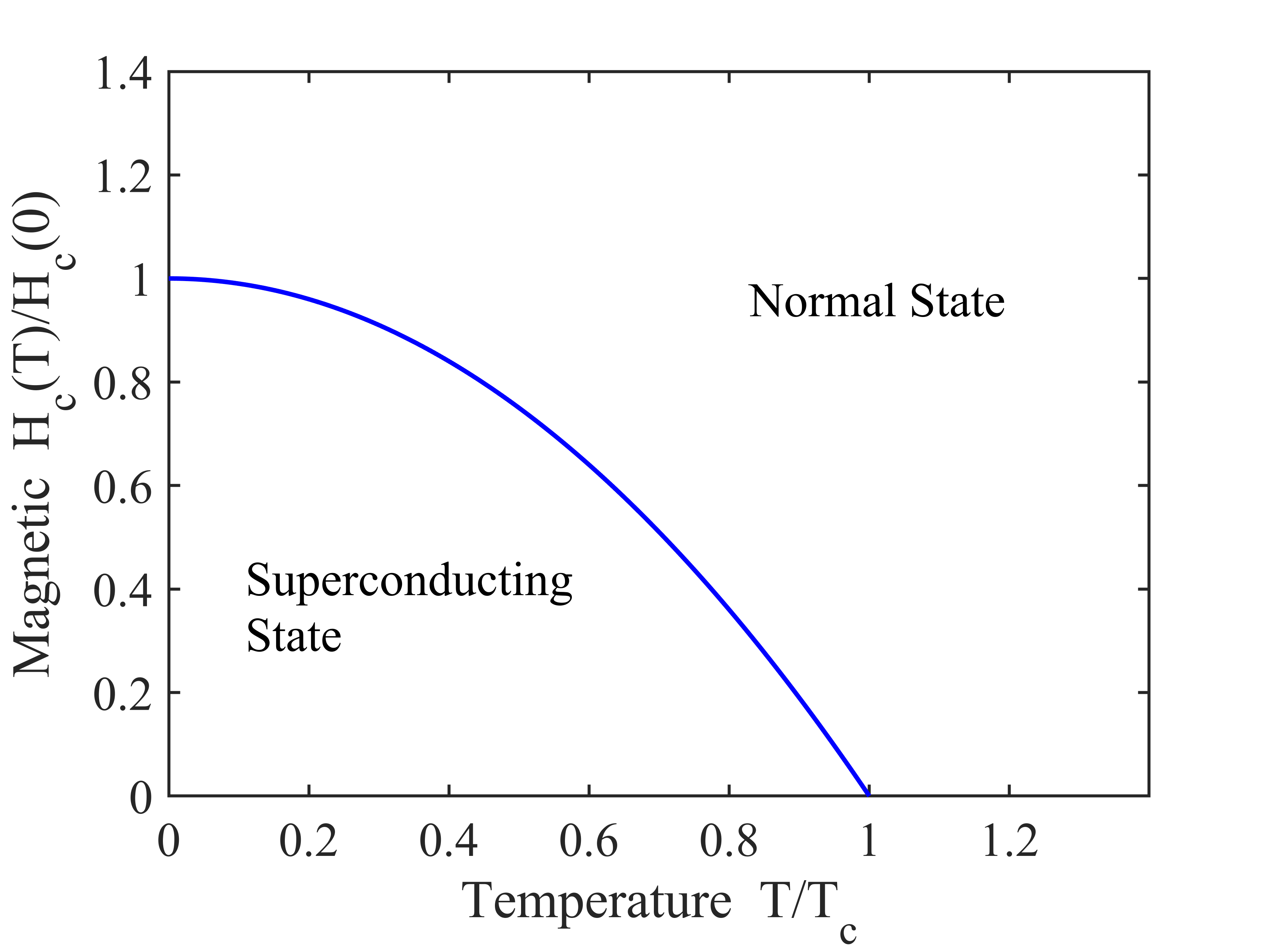
图1. 外磁场下超导态-正常态转变相图

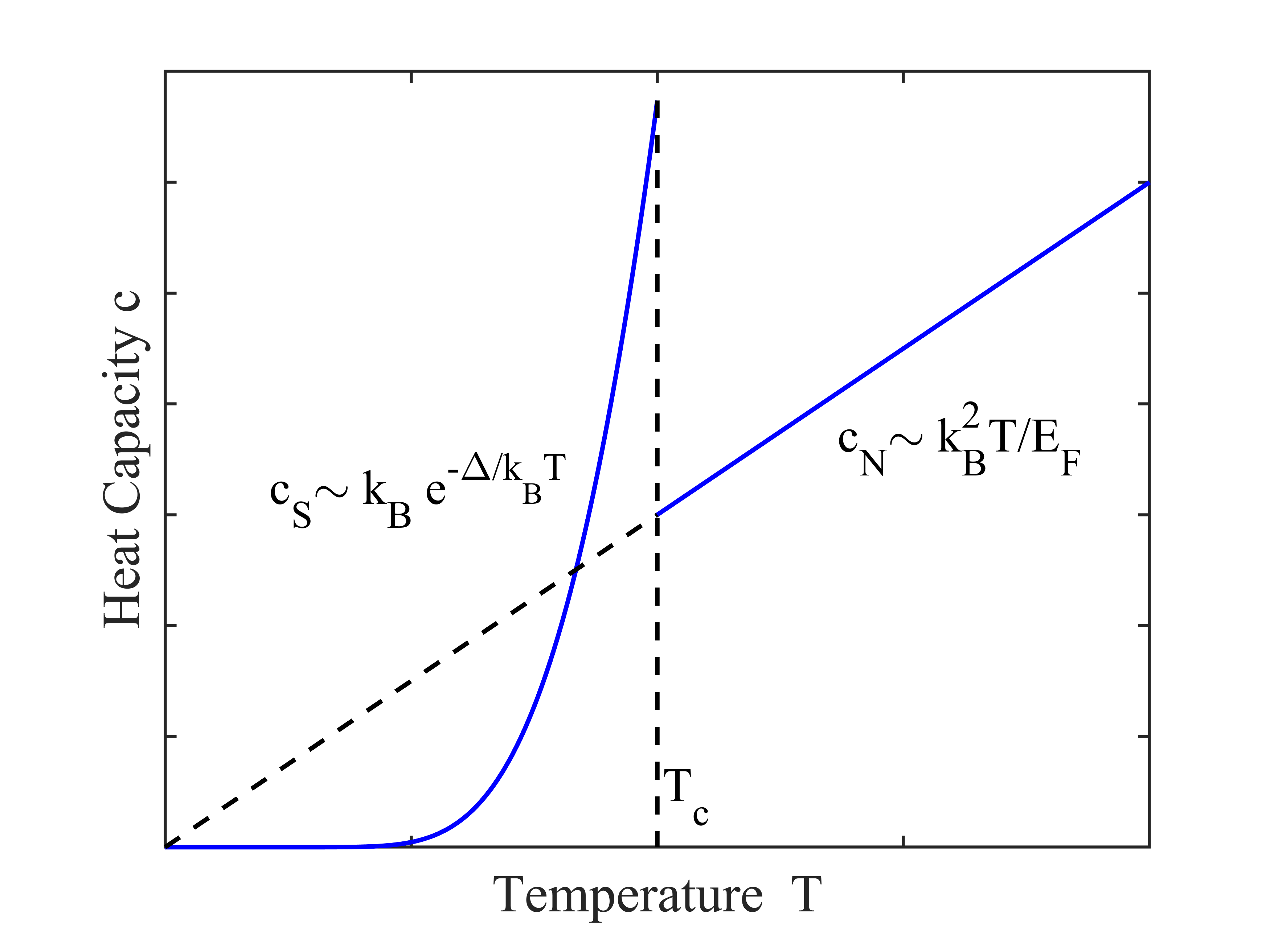
图2. 超导体临界温度附近的电子比热容

根据超导体零电阻特性,人们认为超导体是一种理想的导体.考虑到理想导体内不能存在电场,利用麦克斯韦方程组可以得到,即超导体中不存在变化的磁场,即材料内部保持电阻消失时的磁场,也可以说磁通被“冻结”在导体中.这种“冻结”的概念一直被沿用,1933迈斯纳的实验从事实上否定了这种观念,表明不论是否存在外加磁场,当材料从正常态转变为超导态,只要,导体内部总有.当对超导体施加磁场时,超导体内部不出现净磁通密度的特性被称为完全抗磁性,或者称为迈斯纳效应^[4].这一点表明超导体根本上与理想导体的不同.迈斯纳效应是超导体另一个重要的特性.

除了零电阻效应和迈斯纳效应,超导相变中还会出现其它现象.例如超导态的电子热容 ,而正常态的电子热容正比于温度,如图1 可以发现在超导相变的临界点存在热容的跳变,即这是一个二级相变的过程.另外超导热容的指数因子表明超导态中存在能隙^[2],即从基态激发到第一激发态至少需要的能量.另外使用金属的同位素改变金属离子的质量发现临界温度与离子质量相关即,即同位素效应,这表明电子-声子相互作用在超导起着非常重要的作用.超导能隙和同位素效应为超导微观解释提供了重要的启示,直接影响了BCS理论的建立.

伦敦唯象理论

虽然超导体出现特殊的电磁现象,但是仍然在麦克斯韦方程组的适应范围.而伦敦方程便利用了麦克斯韦方程组给出了超导电流与和的本构关系,从而唯象的描述了超导电性和迈斯纳效应^[5][6].

当材料处于超导态时,考虑二流体模型,可以将超导体中的载流子分为正常传导电子和超导电子,其中超导电子不受晶格散射而没有电阻效应.两种电子的运动形成传导电流和超导电流.其中正常传导电流满足欧姆定律,即满足.而超导电子运动不受阻力,其经典动力学方程为

其中为超导电子质量和电荷,为电子平均速度,为平均电场强度.若考虑超导电子密度为,此时超导电流的微观表达式可以写为,将方程两边对时间微分,并利用方程可以得到:

这就是伦敦第一方程.利用这个方程可以解释超导电性.若考虑恒定电流,此时,容易证明,此时电流完全来自于超导电子而没有电阻损耗;考虑,此时,即在交变电流下存在电阻损耗,此时超导电流密度与正常电流密度的比值为,其中为电流频率,可见对一般低频电流,超导电性仍然近似满足.

现在需要进一步给出关于磁场的方程,从而解释迈斯纳效应,即超导体内部不存在磁场.可以取伦敦第一方程的旋度,并利用法拉第定律得到:

可知不随时间变化,伦敦假设这个量为零,于是立即可以得到:

即伦敦第二方程,伦敦方程唯象的给出了超导体的电动力学. 接下来便是利用伦敦方程解释迈斯纳效应.考虑电流恒定的情形,前面已经知道,此时有方程,对这个方程两边求旋度,并利用磁场的散度为零,以及伦敦第二方程可以给出关于磁场的微分方程:

考虑的半空间为真空,存在恒定磁场,若的半空间为超导体,利用上式便能得到超导体内的磁场为.通常,可见磁场在超导体内随着指数衰减.其中也称为伦敦穿透深度.这样我们就解释了迈斯纳效应.另外通过伦敦方程也可以证明超导电流主要存在于超导体表面厚度约为的薄层内.伦敦方程给出了超导态的电磁描述,关于超导相变以及超导微观机制,后面我们将进一步说明.

金兹堡-朗道理论

在伦敦方程中超导电子密度与磁场及空间位置无关,因此仅适应弱磁场中的均匀导体,而处理非均匀超导体以及强磁场可以使用金兹堡-朗道(G-L)理论^[3][7][12].1950年金兹堡和朗道革命性的提出用一个复序参量来描述临界温度以下的超导体,且序参量的模方为超导电子局域密度,可以知道对于正常态,而超导态.在临界温度附近,序参量是一个小量,根据朗道的二级相变理论^[8],当外场为零时可以将自由能密度按以和的幂展开:

方程中的表示超导电子的质量.若考虑电磁场的影响,可以将梯度算符替换为,这里的表示超导电荷.同时在自由能密度添加磁场的能量,这样可以将自由能密度改写:

上面就是考虑电磁场后G-L自由能密度,而整个超导体的自由能为上式对空间的积分即.利用热力学平衡条件,要求自由能能取得最小值,考虑是和的函数,可以分别对进行变分,并考虑自由能的变分为零,这样我们便可以得到下面两个方程:

这就是金斯堡-朗道(G-L)方程,其中第一个关于的非线性量子力学方程,第二个方程是量子力学中的电流密度公式.当然除了以上两个方程,还可以得到两个源于积分假设的边界条件,文献有详细说明.若假设弱磁场的条件,此时在空间基本均匀分布,可以得到,此时有,将其代入第二个方程,并对两边求旋度,考虑梯度场的旋度为零即,可以得到:

方程中的定义见前面的方程.可以看出在若弱场近似下通过G-L理论可以得到伦敦第二方程.

现在我们考虑G-L方程的一个特殊解,令外磁场为零,此时,此时超导电子密度空间均匀,此时有序参量可以看成实数且空间均匀,这样G-L第一方程化简为,容易得到方程的两个解^[9]分别为:

需要说明为了保证,当时有,而当有.即当连续的从变化到时,参数连续的从小于零变换到大于零,且,而参数始终大于零.这样可以将参数在附近泰勒展开:

下图3,4 分别给出正常态和超导态时,超导与正常态自由能密度之差随序参量的变化,可以看到取得最小值时序参量并不相同,且最小值也不相同.

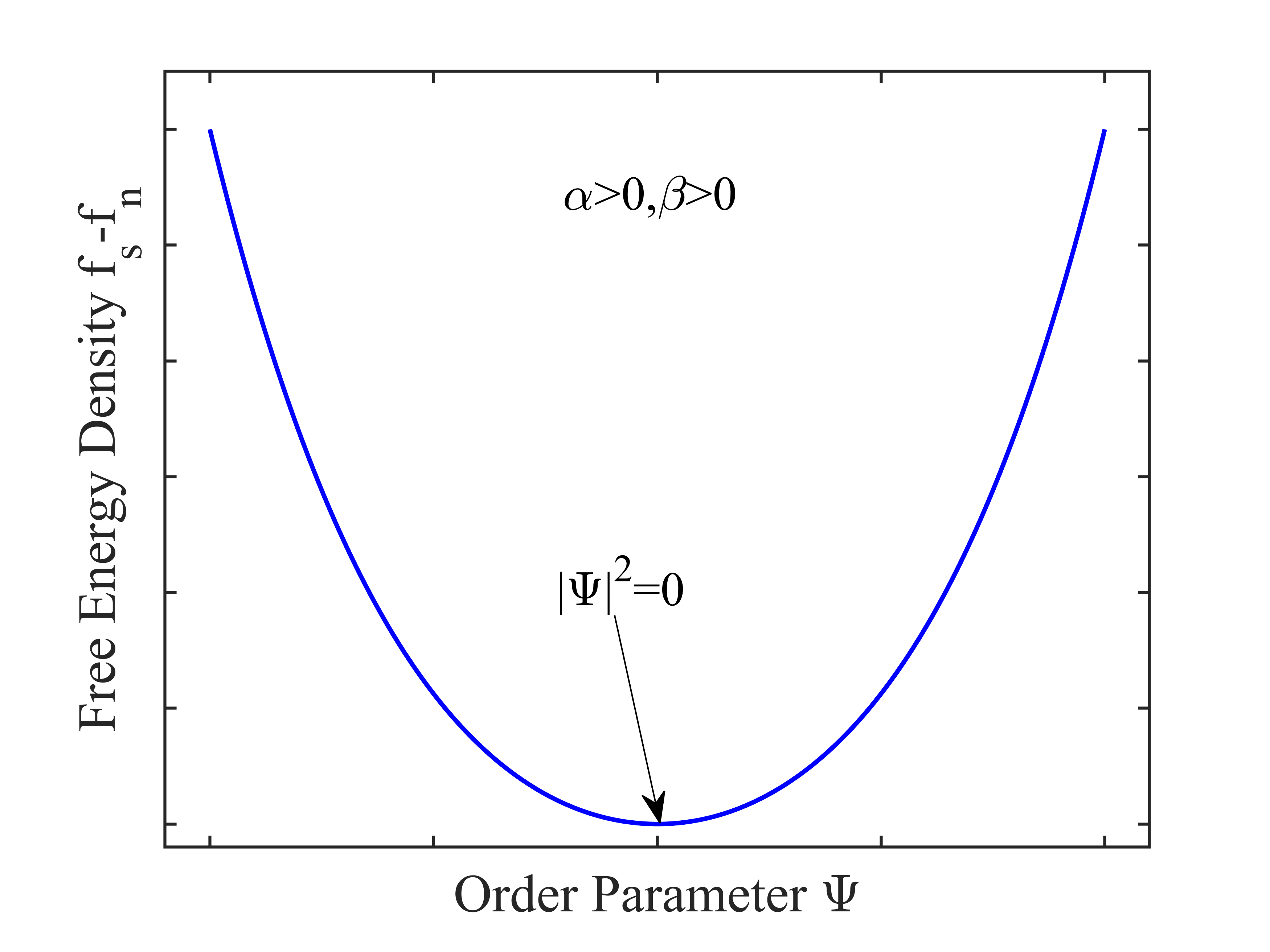
图3. 温度高于转变温度,自由能密度之差

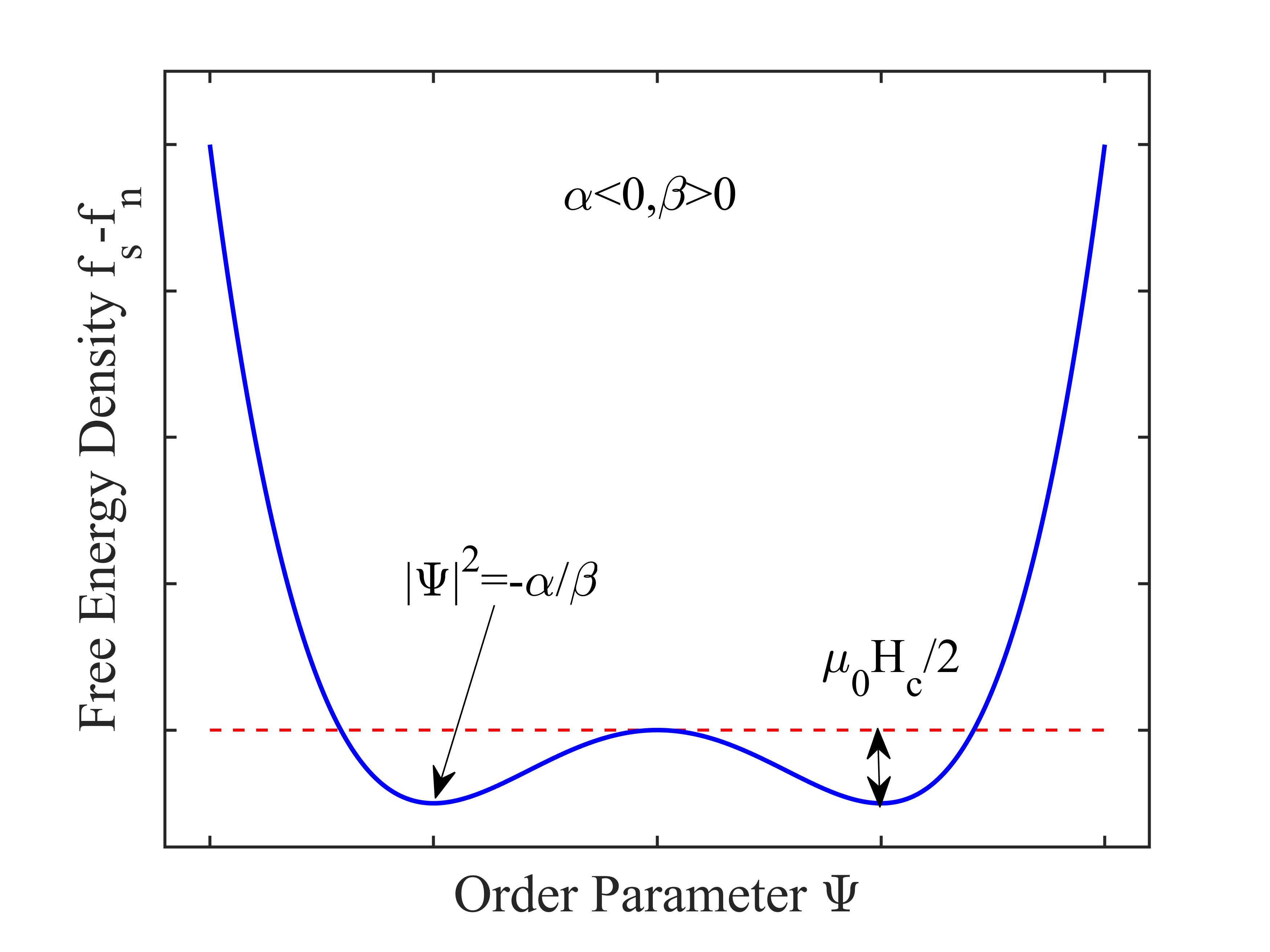
图4. 温度高于低于温度,自由能密度之差

计算可得从超导态转变为正常态,自由能密度之差为:

其中方程中的第二个等式来源于热力学,即是有序超导态的凝聚能,这里为热力学临界场.在临界温度附近考虑参数的泰勒展开式,代入到上式可以得到:

这和前面的经验公式在临界温度附近的近似式一致.同样结合前面的公式可得到的表达式,也与经验公式在的公式一致.

前面我们已经讨论了在无外场且均匀的情况下G-L方程实常数解.现在我们考虑在弱磁场下,此时序参量在空间会缓慢变化,且非常接近常数解,任然令,并引入一个量纲为1序参数定义为:

考虑到满足G-L方程第一,即可以得到序参数满足下面的方程:

由上式可以很自然的可以定义一个特征长度为:

这里的为G-L相干长度,这样就可以将前面的方程简化为,考虑方程的边界条件,可以得到方程的解析解为.下图5 给出了序参数在超导体内部的变化情况,可以发现在超导体表面深度为左右序参数变化明显,而当时超导体序参量,即为均匀超导态,这是由于磁场在超导体表面深度迅速衰减,即在时几乎不存磁场,此时又回到前面我们所提到的情形.

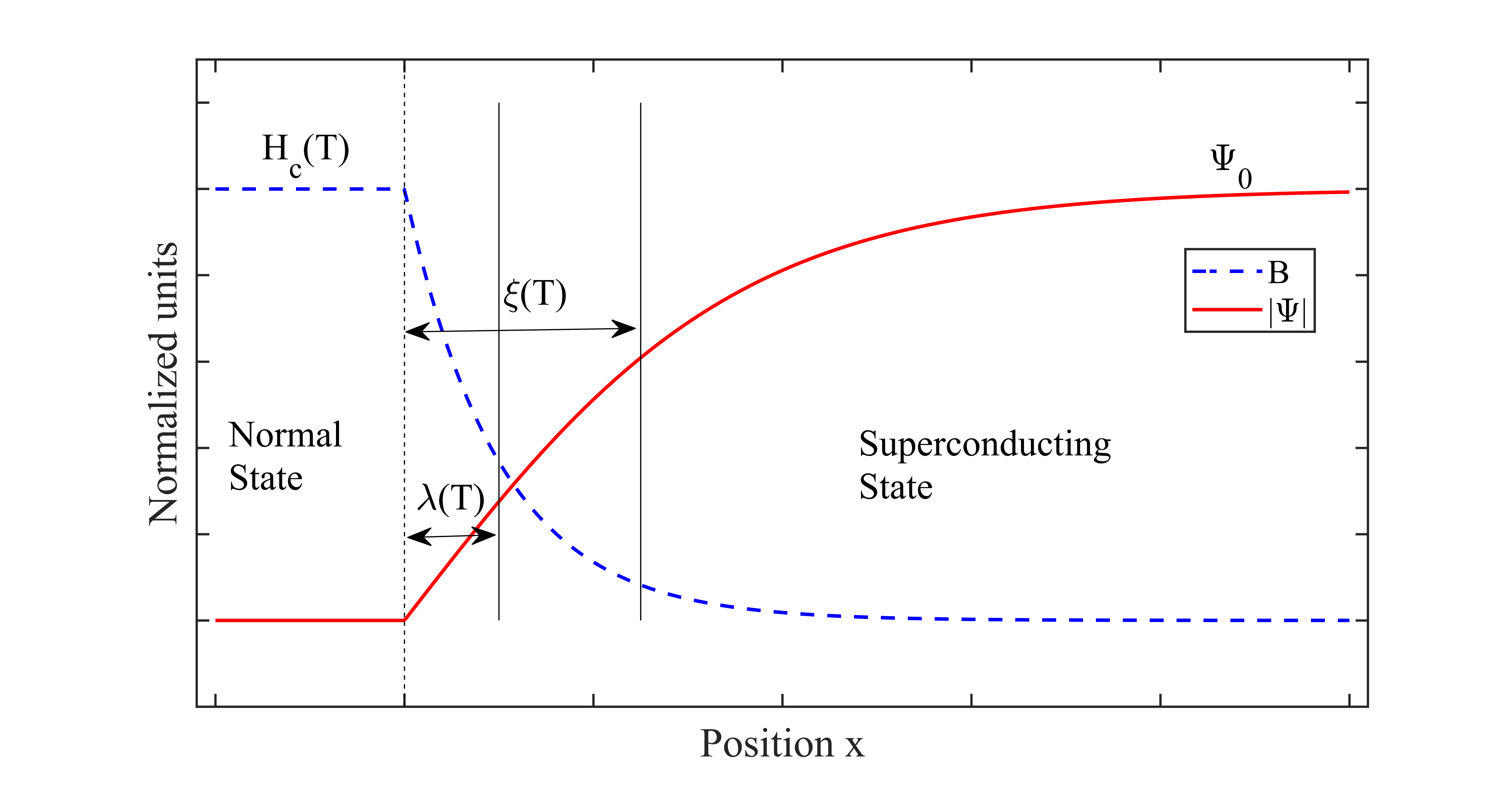
图5. 正常导体与超导体边界序参数与磁场的变化

这里的磁场穿透深度由仍然由前面的公式所定义,当然和相干长度是不同的概念.考虑到在弱磁场中,这样可以将穿透深度可以修正为:

可以看到当温度在临界温度附近,与G-L相干长度表达式表达式相似,都与成正比,若将比上可以得到一个无量纲的参数为:

这个参数也被称为金兹堡-朗道参量.
利用前面的等式,可以得到一个重要的关系式:

这里简单的说明一下G-L参数是超导体分类的重要参数,当时,超导体的界面能,为类超导体;而当时,超导体的界面能,为类超导体.关于超导体的界面能以及超导分类在文献中有详细介绍,这里不再赘述.

以上通过在弱场条件下对G-L方程的分析,可以看到G-L方程同时引进了超导体的穿透深度和相干长度两个重要的参量,它是对伦敦方程的有效推广,同时也包含皮帕德理论的主要内容.最重要的时G-L给出了超导最一般的描述,当然关于序参量的物理意义以及微观解释并不能直接得到,这是后面的内容.

低温超导的BCS理论

二流体模型已然指出超导相变后,超导相的秩序度是由超导相中的电子发生某种序变化引起,而G-L理论引入的相干长度以及界面能等,都显示这种序是长程序.而超导电子的指数比热,则表明的超导态电子能谱有能隙的存在.另外同位素效应进一步反应了电声相互作用在超导态中的关键作用.这些都为超导的微观物理图像的建立奠定了基础.1956年库珀^[10]提出的电子对束缚态完成了超导微观理论的关键一步.

现在我们介绍库珀的双电子模型^[2][11],设想在绝对零度将一对电子加入金属中,这两个电子只能处于费米球外面,它们通过声子以及库伦场进行相互作用,忽略晶体能带结构仅用体积为的盒子代替周期性的势场,对于双电子系统的完备集,可以取平面波的直积,显然这个这个波函数满足周期性边界条件.若定义质心和相对坐标为和 ,这样我们可以系统的波函数设为完备集中所有态的线性叠加:

在质心坐标系下,可以将带相互作用的双电子模型的哈密顿量写为,现在可以将波函数代入到薛定谔方程后可以得到:

其中电子对的能量表示为,这里一对电子从动量态散射到动量态的位势强度,且这个过程总动量守恒.通常这个方程难于求解,库珀引入了如下近似:

其中满足(称为截断频率).也就是说在费米能以外,以内电子具有吸引相互作用.在这种近似下将极大的简化方程的计算,代入到方程可以得到下面的方程:

这里表示总动量为,能量为的双电子态的密度,由于双电子能量变化范围小,密度可以近似为.考虑近似后可以将密度放到积分外即:

计算可以得到本征能为,这里为电子对的结合能.可以看到能量低于.需要说明的是对于费米面外面五相互作用的粒子其能量必然大于,当两个电子之间存在净吸引位势时,都可以形成一个库珀电子对,其能量低于,这使得材料中原有的电子可重新组合,使得更多的电子构成库珀电子对,进入比费米海能量更低的稳定状态,人们预期这将导致出现超导基态.另外库珀对的扩展范围远大于粒子间的平均距离,即显示处一种长程序.最后需要说明的是当时,允许散射的态数目最多,如图允许散射态的数目与交叠面积成正比,即取得最大值,也就是说电子对动量态满足时得到的能量降低最大.

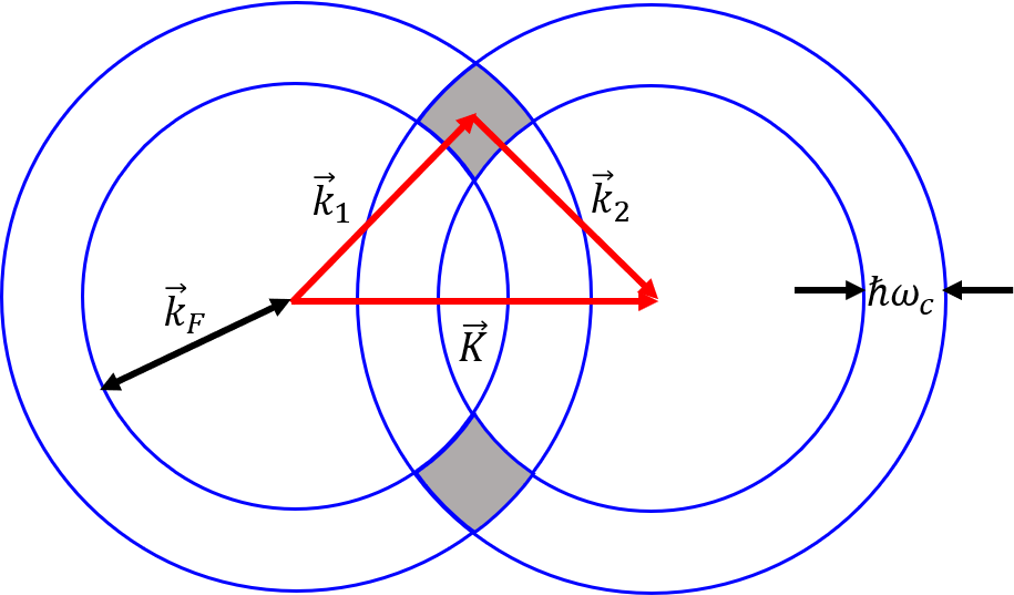
图6. 总动量为K电子对的吸引区

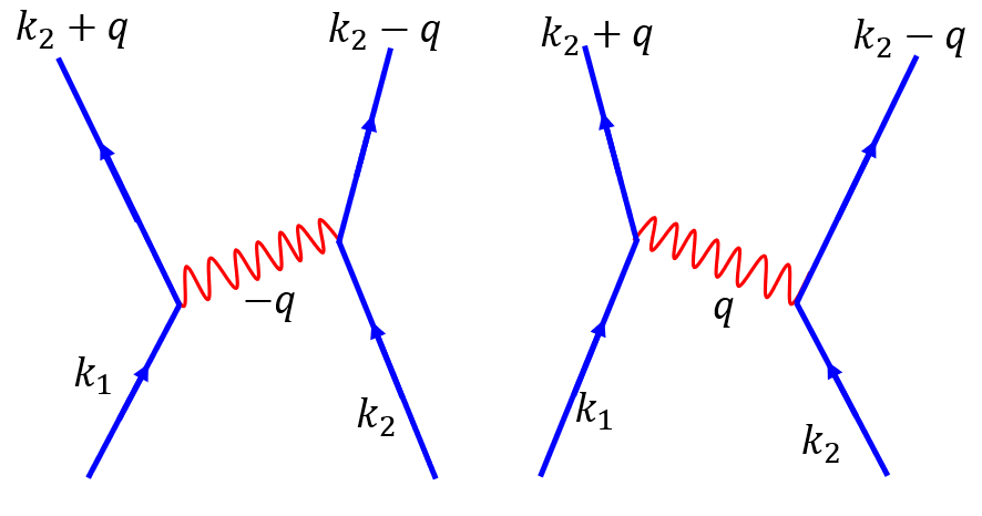
图7. 电子-声子-电子相互作用

在库珀电子对的基础上,巴丁、库珀和施瑞弗进一步将的库珀的双电子模型进一步推广到多电子系统,并用于解释超导现象,这个理论也被称为BCS理论.其中BCS理论的基础便是超导体费米面附近的电子形成库珀电子对从而降低系统的能量.前面已经说明库珀电子对的基础是电子间净吸引的相互作用,相互作用包括电子间排斥相互作用(Fermi-Thomas近似),以及由声子耦合的电子-电子相互作用,如图7 所示.因此形成库珀电子对需要满足:

从这个式子可以看出在超导中电声相互作用的重要作用,而声子是由于原子实振动产生,即可以解释超导的同位素效应.接下来将讨论超导基态波函数的形式,引入二次量子化的算符分别表示电子的生成和湮灭,满足反对易关系.在库珀电子对的基础上,BCS理论考虑超导的基态由电子对形成,且电子对动量相反,自旋相反.引入库珀对生成算符以及湮灭算符.同时BCS采用了类似Hatree近似的方法建立基态波函数,即不同的电子对态独立:
这样可以将基态波函数写为对态占据和未占据的叠加态:

这里表示电子对态占据概率振幅,且满足.表示真空态.接下来我们需要考虑BCS基态的能量,当然需要给出多电子系统的哈密顿量,由于BCS理论考虑基态只有电子对态,此时相互作用仅包括电子对之间的散射即可以将哈密顿写为:

第一项为自由电子哈密顿量,第二项为相互作用项,其中相互作用强度仍使用前面的近似.将BCS波函数和哈密顿量代入到薛定谔方程,便能得到能量的表达式,然后利用变分法得到能量极小值,具体计算见文献.计算得到的超导基态能量为:

为正常金属基态能量,表示费米面电子的态密度.只要存在净吸引,超导基态能量会低于正常金属基态能量.是时的凝聚能,由热力学理论.

现在我们进一步考虑粒子激发的情形.对于对态有一个态且仅有一个态的单准粒子激发时,所需要的能量为,可以当激发能最小为.而破坏每一个库珀电子对的单粒子激发会产生两个准粒子,最小的激发能量为.也就说超导的基态到第一激发态存在一个能量为的能隙.考虑在零温附近,电子都形成了库珀对,此时激发能量只能为,此时系统类似一个二能级系统,可以简单的得到超导电子热容,与前面前面提到的电子热容一致.需要说明的以上关于BCS理论的讨论都是在下进行的,很自然可以推广到时的超导,这里我们不再赘述.

以上我们用BCS理论解释了超导体的热力学性质,那如何用BCS理论理解超导的零电阻现象呢?当无外场时,库珀对的总动量.当外加电场时库珀对在外场作用下有一个动量整体平移,即库珀对从变为.由于超导体中电流由库珀电子承载,即电流密度为,而电子晶格的散射等效为库珀电子对的散射,这种散射保持总动量守恒,即电流不会衰减,宏观上表现为零电阻.

总结

本文首先介绍超导的基本特征,包括超导电性,迈斯纳效应,超导电子热容特性,能隙,同位素效应以及超导的临界现象.为了描述以及理解超导体,出现了许多理论,从宏观到微观,从唯象到具象.最早的伦敦方程基于超导的二流体模型和超导的宏观电磁特征解释了超导体的零电阻特性以及完全抗磁性.G-L理论则从朗道的二级相变理论出发给出超导序参量的G-L方程以及超导电流精确表达式.BCS理论则完全从微观的角度出发,利用库珀电子对刻画了超导体的微观图像,解释了超导能隙,超导同位素效应等.