1. 引言
2. 光线弯曲
   1. 基于经典理论的光线弯曲
   2. 基于弯曲时空的光线弯曲
   3. 史瓦西黑洞附近的光线弯曲
3. 黑洞背景

引言

对于大质量的天体,导致的时空弯曲效应不可忽略,特别是对于黑洞这种极端的天体,强大的引力作用可以使光线完全偏离原始方向,甚至不能逃逸引力吸引而落入视界。

光线弯曲

在引力作用下光子如何运动,虽然光的静止质量为零,在经典框架下任可以考虑引力给光子的加速度,这是因为引力产生的加速度与物体本身性质无关,因此在经典背景下可以用牛顿方程描述光子运动。在广义相对论的框架下,引力导致时空背景弯曲,而光子在时空中沿测地线运动,因此弯曲时空的测地线方程即能描述光子运动^[1][2]。

基于经典理论的光线弯曲

在极坐标下,经典理论给出引力背景下粒子的运动方程满足 ^[2] :

其中为粒子角动量,对于经过大质量天体附近的光子,其角动量为 ^[4],考虑代换,即得到天体附近光线方程为:

若,可以将其视为微扰,不考虑微扰情况下,方程的解为直线,考虑微扰即得到方程的严格解为:

考虑在无穷远处,即时,方位角为其中,代入解中得到:

可得到,以及光线经过天体附近的偏转角为:

即得到了经典情形下光线偏折角度,当然这个结果与广义相对论给出的结果并不相同,后面可以看出两者的区别.

基于弯曲时空的光线弯曲

对于平直时空,光线沿直线传播.对于弯曲时空,光线传播的最短路径为测地线,即满足测地线方程^{[1] [2] [5]} :

这里为仿射联络(克氏符),可以通过时空度规得到.对于静态的各向同性的引力场,度规的一般形式 ^[5] 为:

其中度规中参数 由场方程的解所决定,这里考虑静态球对称的真空解即史瓦西解,里奇张量,史瓦西解对应的度规张量为:

仿射联络可由度规得到:

根据上式得到史瓦西时空,仿射联络的非零分量:

考虑到引力场的对称性,可将光线的轨迹限制在赤道面上,即,将上述分量代入到测地线方程,可以得到以下方程组:

将分别除以后面两个方程,积分后可以得到^[5] :

其中均为积分常数,或称为能量和角动量^[2] ,将以上结果代入第一个方程得到:

将上式乘以,并对积分可以得到:

利用以上方程可以消去参数得到描述光线路径的方程^[2] :

其中积分常数可以吸收进.此方程给出了光线在赤道面内的运动方程,做变量替换,得到:

当不存在引力场即时,上式退化为平直时空光线的轨迹方程,解为直线。对于一般天体,方程右边可以做为小量处理,将零级解代入方程右边,得到:

可以得到上式的一个特解^[2] :

即得到原始方程的一级近似解为:

考虑无穷远处,,令一级解的方位角为,代入方程有:

可以得到光线偏折的角度为:

即得到了弯曲时空中光线偏折的角度,可以发现偏折角度为经典结果的两倍。反映了两种完全的观点,在相对论的视角下,时空发生弯曲使得光线弯折,在经典视角下,光线在平直时空受到引力作用下发生弯曲。

史瓦西黑洞附近的光线弯曲

对于黑洞这样的天体,考虑到其附近的时空扭曲非常厉害,微扰条件不再满足,上述微扰展开求解的方法不再有效。虽然不能期待得到确定的解析解,但是通过数值求解的方法可以研究光线在黑洞表面弯曲的过程,这里考虑初始条件,这里我们取,下面的是光线以不同角度经过黑洞时的表现:

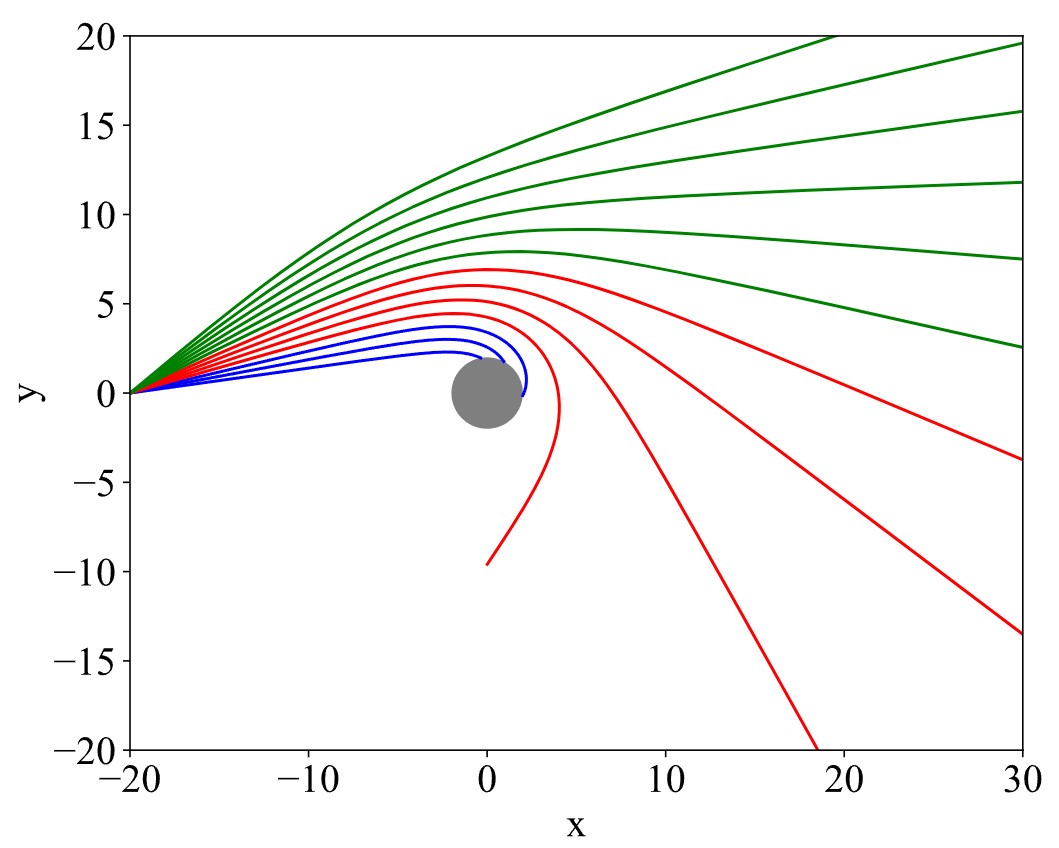
图1.不同角度入射光线在通过黑洞时的表现,蓝色表示以小角度入射的光线落入黑洞视界;红色表示光线发生大角度的偏折,绿色表示大角度入射的光线发生小角度的偏折.

可以看到光线经过黑洞附近,光线发生大角度的偏折,甚至完全改变其传播方向,这是与一般天体大不相同的,这是由于黑洞会强烈的扭曲周围时空,从而导致光线大角度弯曲。

黑洞背景

得到黑洞附近光线的传播情况后,我们就会想黑洞的背面长什么样,这篇博客详细的描述如何计算黑洞的背景 ^[3] ,这里我们简单介绍,假设黑洞的背景上某个点聚焦到相机的焦平面某个点,考虑光线可逆,因此相当于从点以角度发射光线经过黑洞的弯折作用,以到达物点,即可以得到相机中黑洞的背景。其中可以通过前面方程数值计算得到如下图:

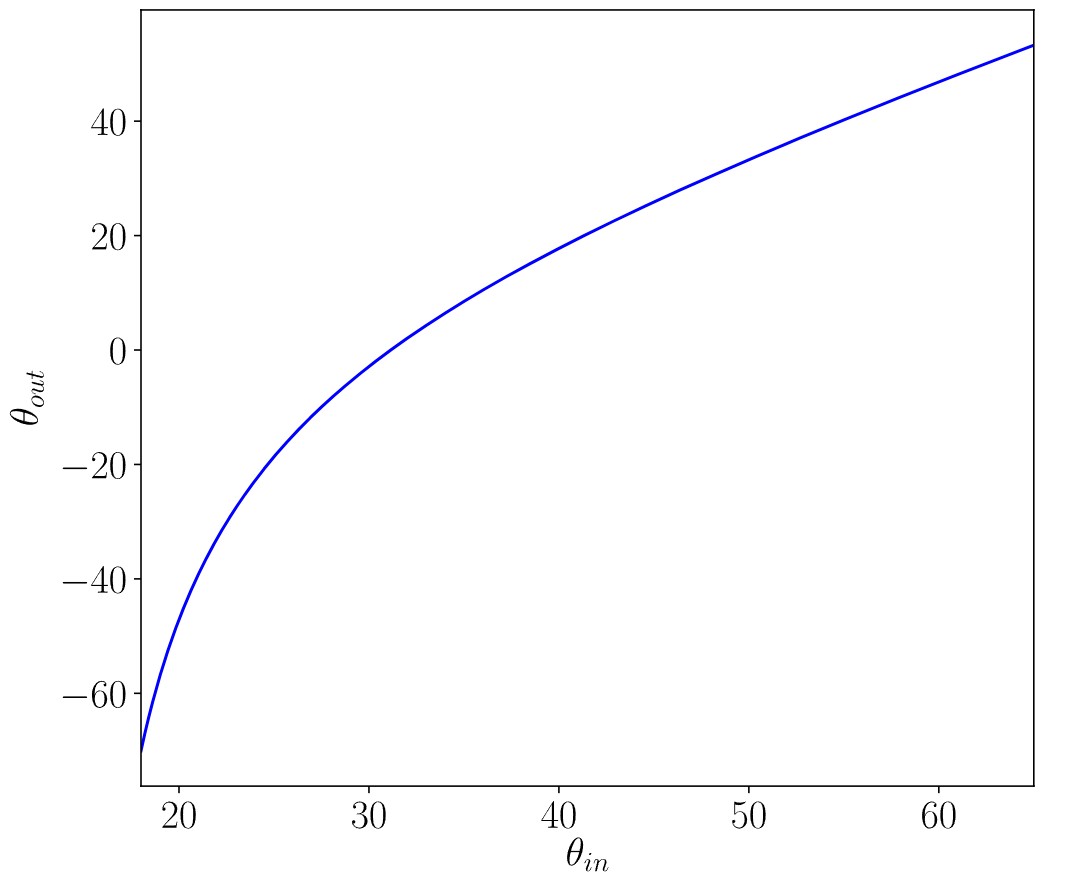
图2. 不同入射角度对应的出射角度

通过以上过程容易得到黑洞背景,以下是计算得到的黑洞背景:

可以看到有一部分背景发射的光线被黑洞吸收或者发生大角度弯折后不能被相机探测到, 且黑洞附近的背景被强烈扭曲,当然离黑洞越远扭曲作用越弱.