Deutsch 算法
定义函数
利用经典算法,需要两次运算才能确定
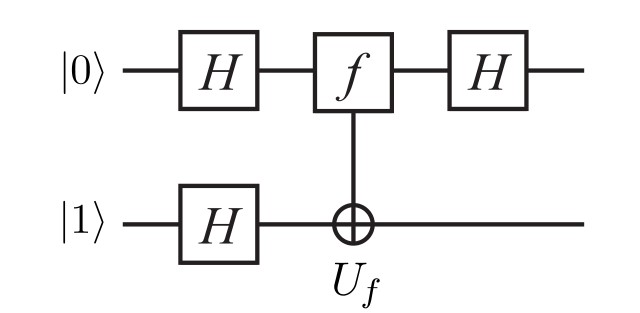
量子态经过
若
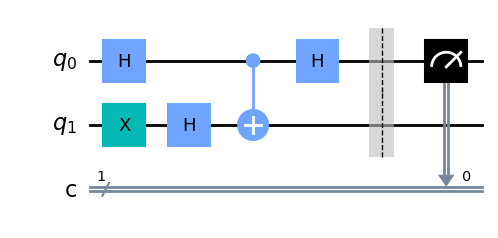
初始量子比特制备在
Deutsch-Jozsa 算法
作为Deutsch问题的推广,定义二值函数
初始化
个q-bits到态 . 对每个q-bits进行Hadamard操作,变换完后的态为:
考虑量子操作(oracle)包含
个控制比特和单个受控比特,即 ,作用于 得到: 然后再作用Hadamada门于前
个比特,得到: 其中
可以记为 ,这里 。 最后一步即测量,考虑态
的权重为: 若
为常值函数,当 时其权重为 , 时,由于 有一半为 一半为 ,求和后得到权重为零。若 为平衡函数,当 时,权重 ,由此得到 态的叠加。即当测量得到 时,可以判断 为常值函数,反之可以判断 为平衡函数。
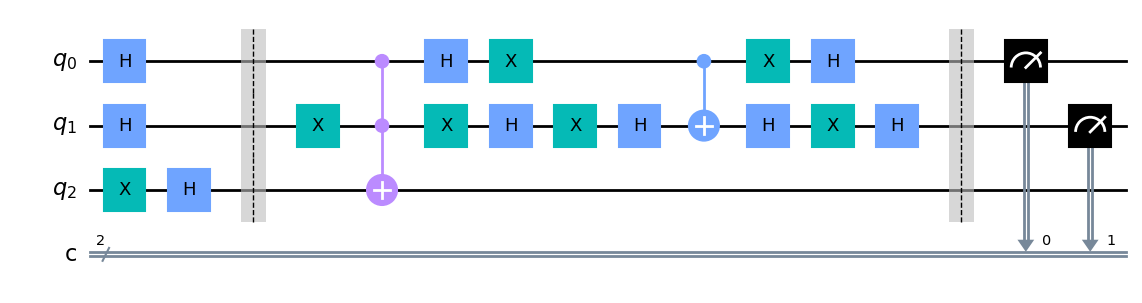
下面给出了一个
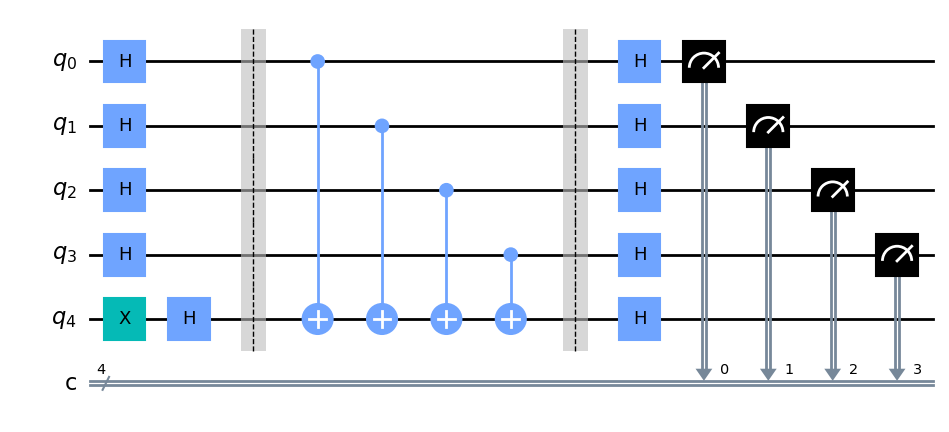
通过运行上述的量子线路可以得到采样结果为
Simon 算法
考虑函数
将
个量子比特制备到初始态 ,然后将Hadamard作用到前 个比特的集合,得到: 考虑量子操作(oracle)包含
个控制比特和受控比特 ,经过 变换后的量子态为: 测量后
个量子比特,若投影到一个确定的态 ,可以知道量子态塌缩到: 紧接着对前
个量子比特进行Hadamard变换得到: 其中
,代入 ,得到:
- 最终再次测量前
个比特,投影得到 ,满足 ,重复量子算法可以得到一系列 ,均满足 ,通过求解线性方程即可以得到周期 。考虑到求解 需要 个线性独立的方程,最好的情况也需要 次重复运行电路,但量子算法的时间复杂度仍是多项式的,相比于经典算法存在指数加速。
Grover 搜索算法
假设一个有
其中
为了实现量子Grover算法,考虑一个量子Oracle ,相当于一个量子黑盒,可以执行如下幺正变换:
其中
若仅考虑
利用量子Oracle可以构造量子搜索算法:
首先制备初态,即等权叠加态(
): 同时将辅助量子位制备到
. 其中目标态振幅为 ,Gover算法的实质就是通过放大目标态的振幅抑制其他态的振幅从而实现目标搜索。 构造对称操作
,可以通过以下三步完成[2] : - 将量子态进行Hadamard 操作。
- 进行相位变换,即
。 - 再对量子态进行 Hadamard 操作。
即。
现在可以构造Grover算法迭代的线路:
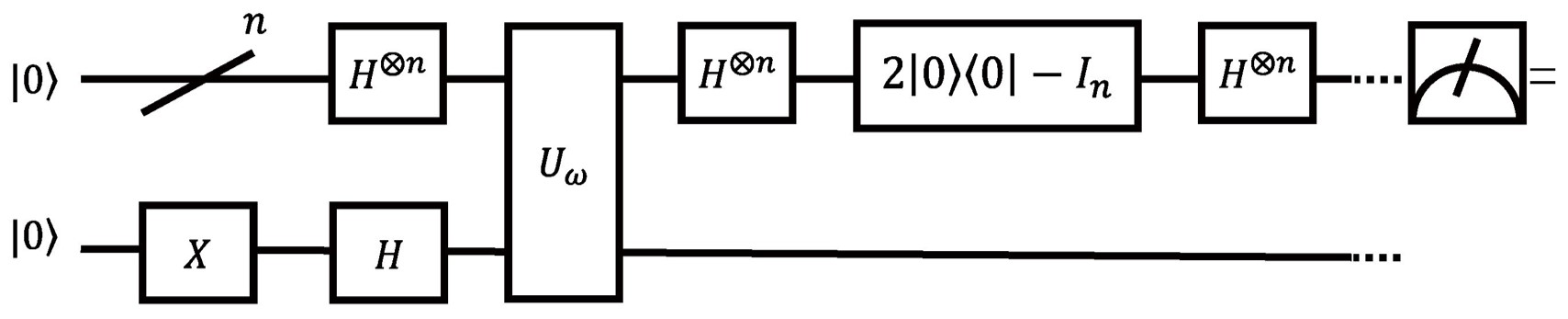
Grover 算法的迭代过程可以通过几何方法理解,其中
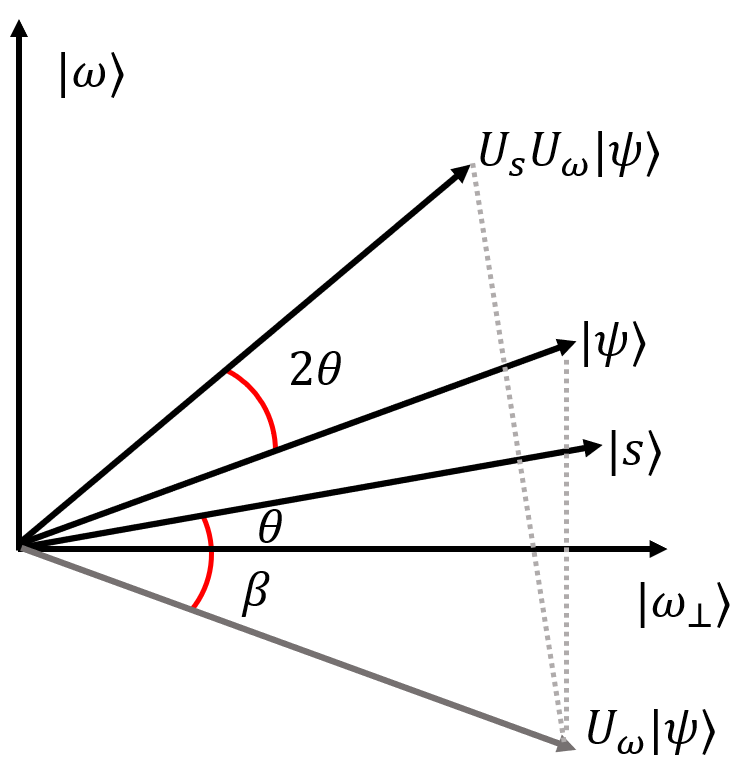
因此经过
可以看到目标态的振幅在迭代过程中变大,考虑迭代结束应该以非常高的概率得到
通常对于一个搜索任务来说,可能存在多个满足要求的条目
同样可以使用Grover迭代,只是每次的旋转角度
构建一个
将初始态制备到
量子傅里叶变换(QFT)
与离散傅里叶变换相同,量子傅里叶变换(QFT)可以定义为如下变换[2] :
QFT就是要通过量子线路实现
可以计算
考虑任意态矢量
接下来要构建量子线路实现上述量子傅里叶变换,首先考虑一个简单的例子即单比特QFT,可以由Hadamard门完成即:
对于多比特QFT,需要利用到控制相位门,即第
可以称为
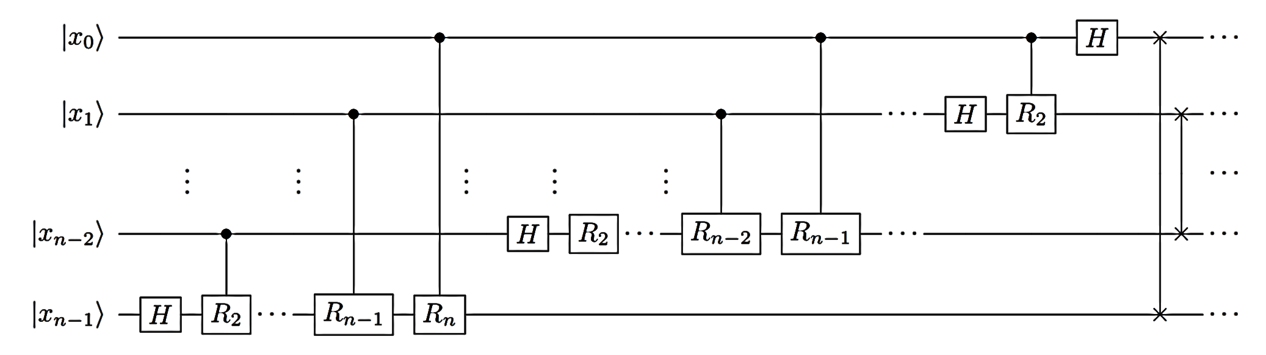
考虑到线路的
考虑一个
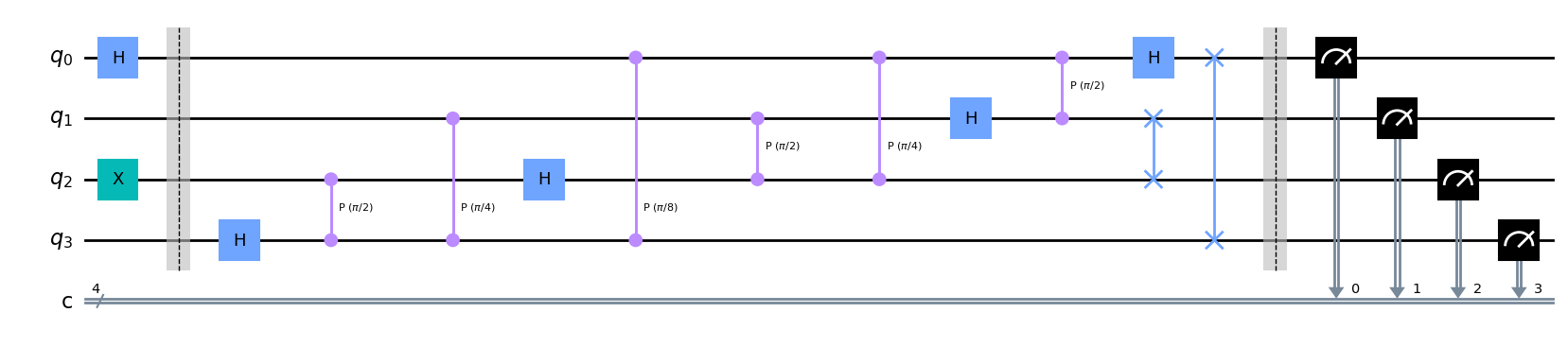
运行此线路
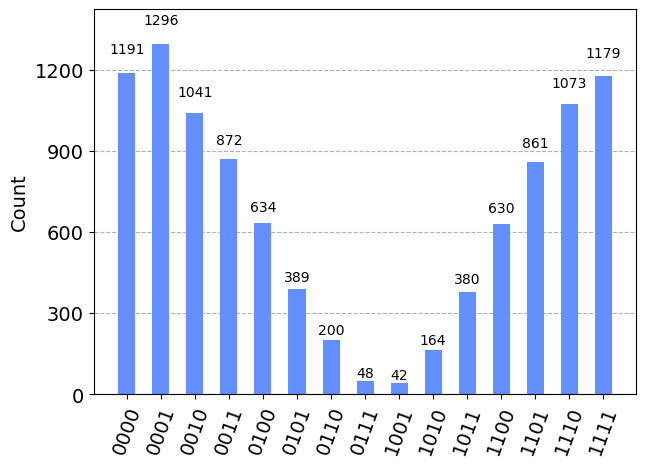
线路运行10000次,做投影测量,每个态出现的次数
考虑一个
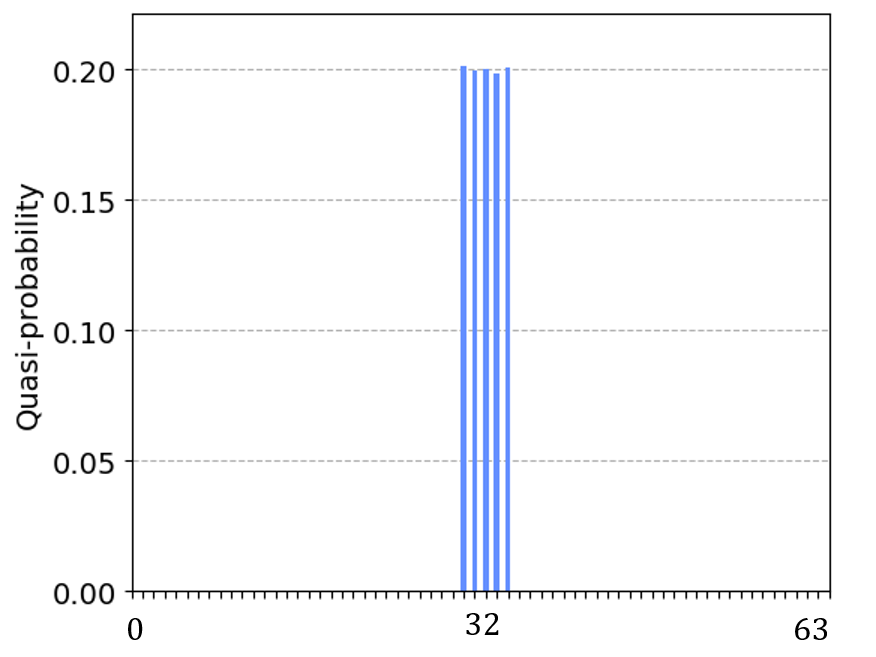
输入态采样后概率分布
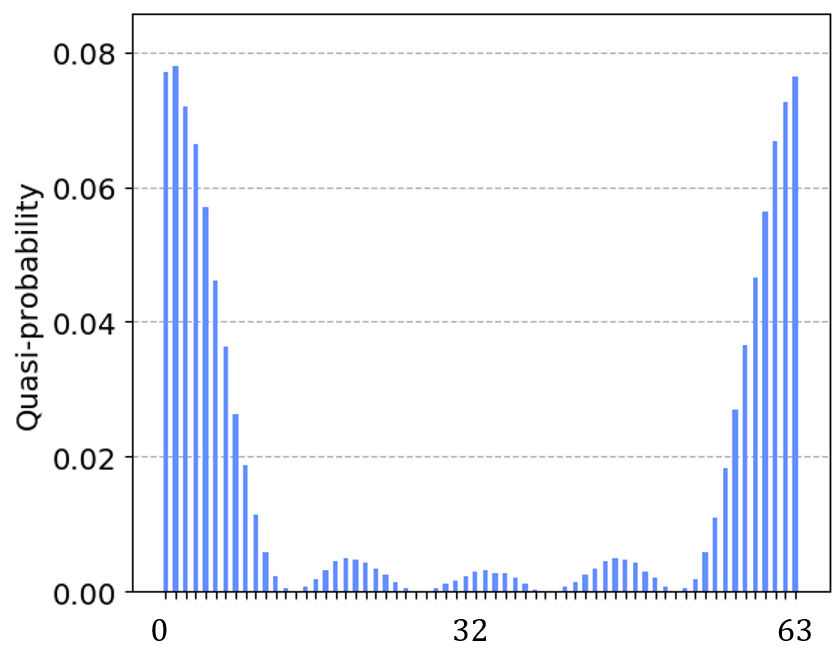
输出态采样后概率分布
量子相位估计
假设幺正算符
为了实现量子估计算法,假设能够制备态
量子相位估计算法需要两个寄存器,第一个寄存器存放相位估计结果,初始化为
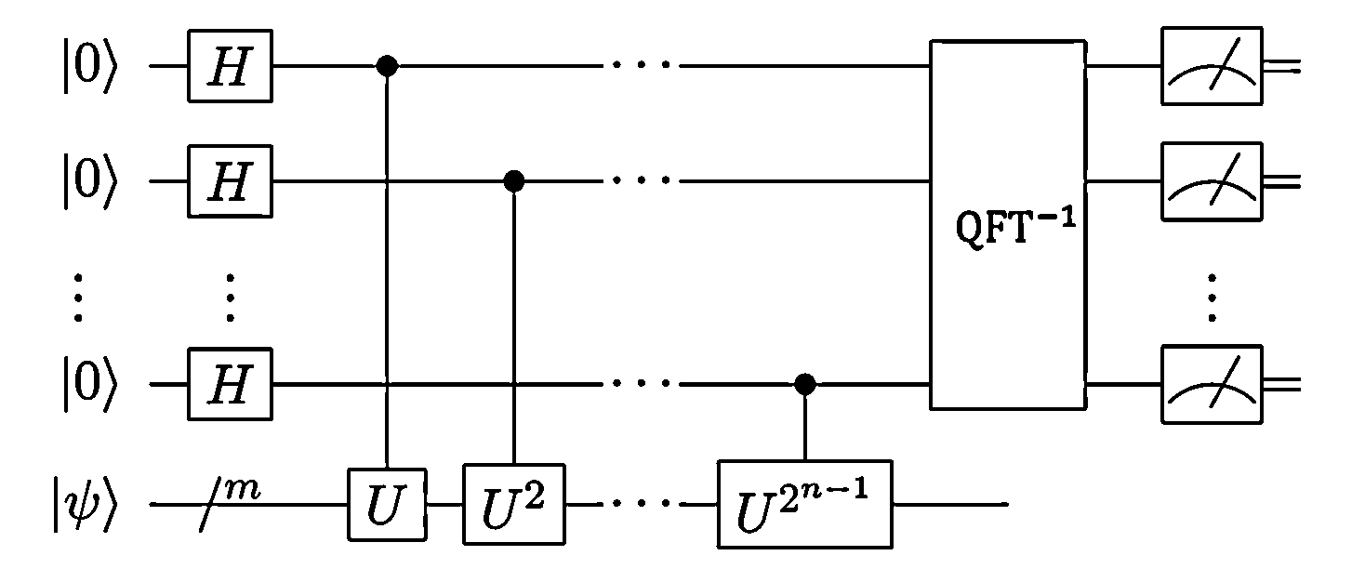
对第一个寄存器的
个比特进行 操作,然后对第二个寄存器进行控制 门操作,其中 的幂次依次为 ,操作完成后第一个寄存器量子态变换为: 由于
,可以将其二进制展开到小数点第 位即:
代入
可以发现
其中
由上面可知,接下来便是执行QFT的逆变换即
对第一个寄存器的所有量子位做投影测量,可以确认目标态
以上的计算都是基于
考虑一个单比特相位门
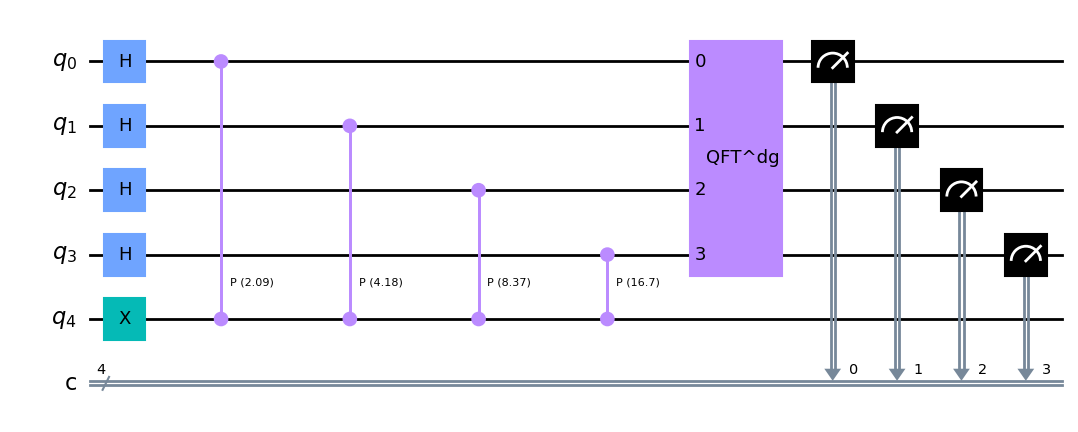
这里为了估计相位的值,使用了
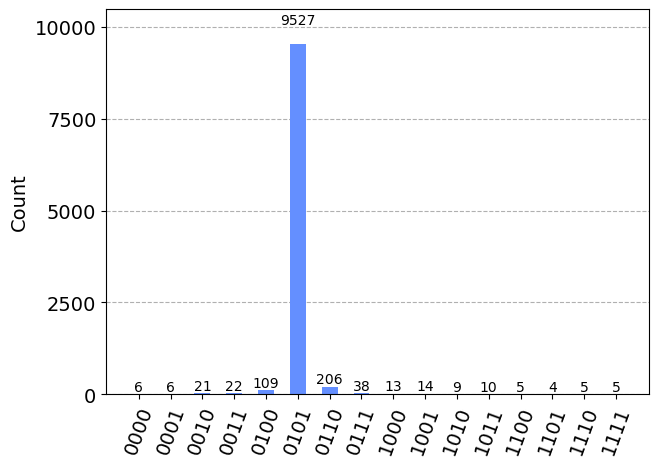
线路运行10000次,做投影测量,每个态出现的次数
可以发现出现概率最大的态为
量子逻辑门
单比特量子门
| 单比特门 | 幺正表示 | 线路图 |
|---|---|---|
| H-gate | 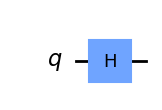 |
|
| I-gate | 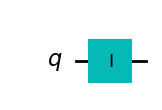 |
|
| Phase-gate | 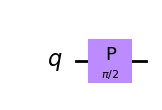 |
|
| T-gate | 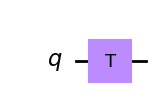 |
|
| S-gate | 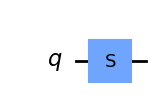 |
|
| X-gate | 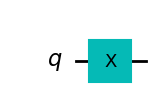 |
|
| Y-gate | 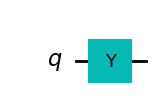 |
|
| Z-gate | 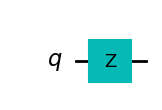 |
|
| Rx-gate | 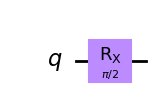 |
|
| Ry-gate | 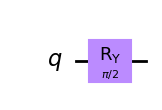 |
|
| Rz-gate | 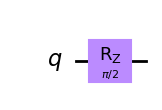 |
|
| U-gate | 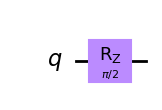 |
多比特量子门
| 多比特门 | 幺正表示 | 线路图 |
|---|---|---|
| CNOT-gate | 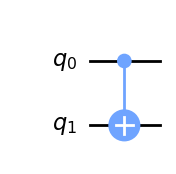 |
|
| CZ-gate | 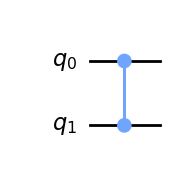 |
|
| CPhase-gate | 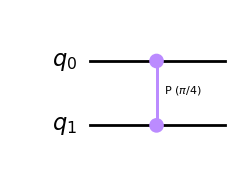 |
|
| CRx-gate | 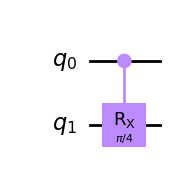 |
|
| CRz-gate | 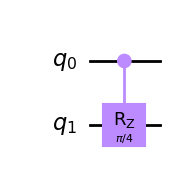 |
|
| CU-gate |  |
|
| SWAP-gate | 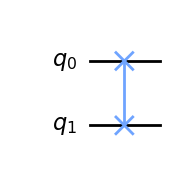 |
|
| Toffoli-gate | 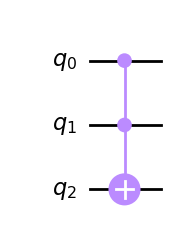 |
- 1.Nakahara M, Ohmi T. Quantum computing: from linear algebra to physical realizations[M]. CRC press, 2008. ↩
- 2.Preskill J. Lecture notes for physics 229: Quantum information and computation[J]. California Institute of Technology, 1998, 16(1): 1-8. ↩
- 3.Benenti G , Casati G , Rossini D ,et al.Principles of Quantum Computation and Information: A Comprehensive Textbook[M]. 2018. ↩
- 4.Nielsen M A, Chuang I L. Quantum computation and quantum information[M]. Cambridge university press, 2010. ↩
- 5.李承祖等编著.量子计算机研究. 上. 原理和物理实现[M].科学出版社,2011. ↩