- 平板波导
- 几何分析
- 波导模式分析
- 光纤波导
- 光纤模式分析
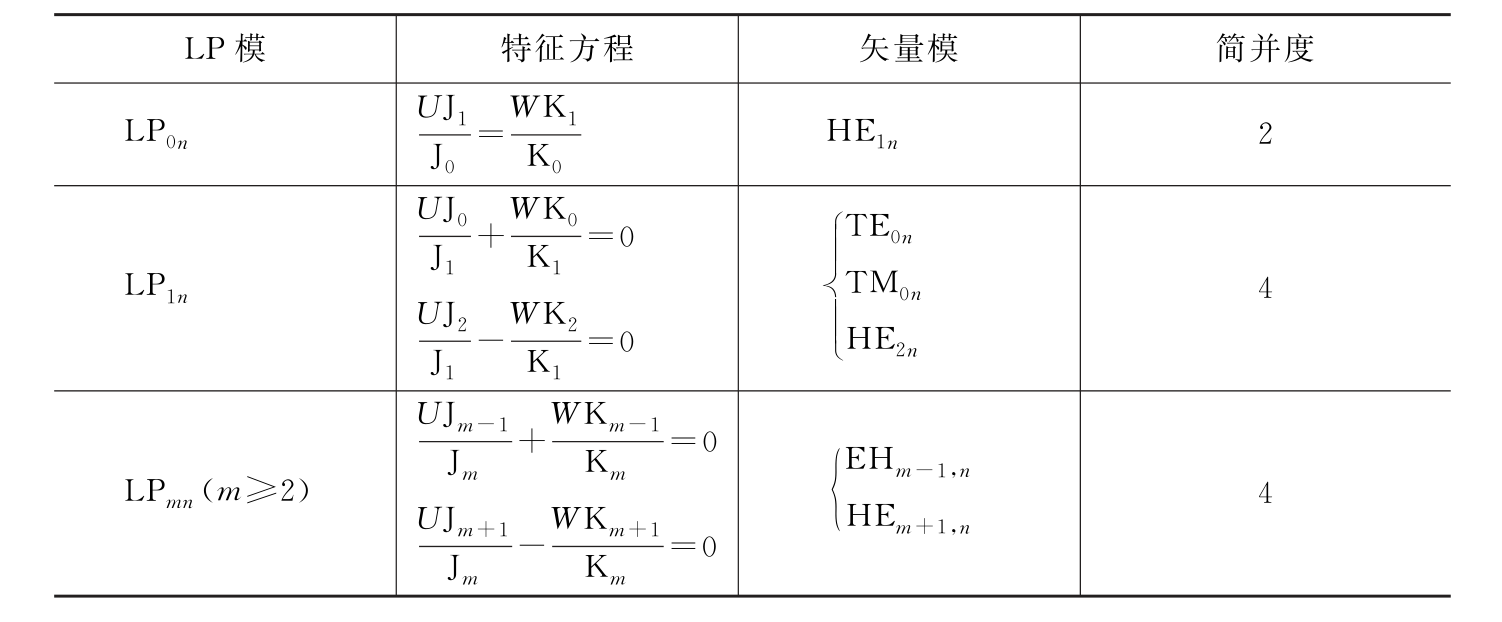
- 模式分类
- 定性分析
- 模式色散曲线
- 线偏振(LP)模
平板波导
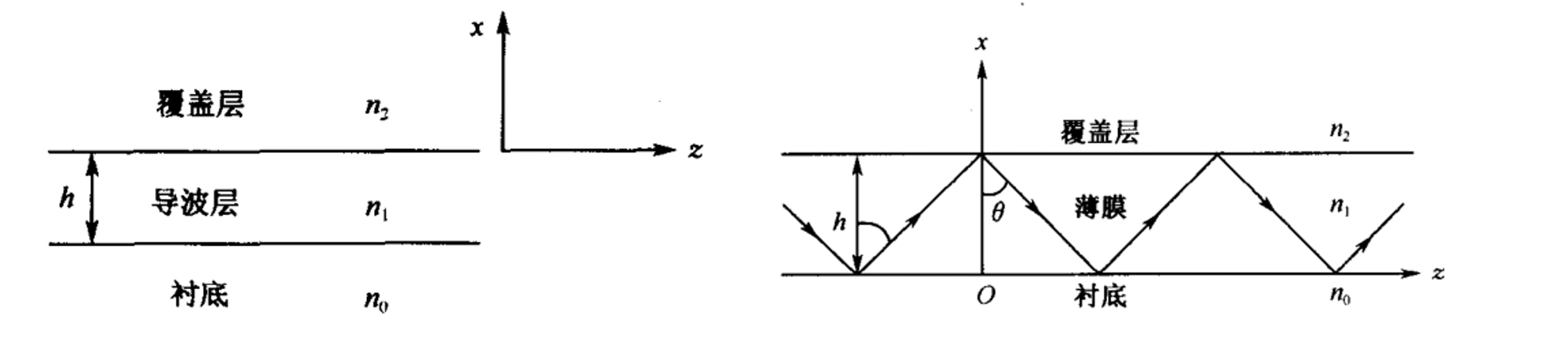
平板波导是最简单的光波导,通常由两层折射率低的介质夹着折射率较高的中间层组成,对平板波导各种性质的研究有助于对其它复杂波导的认识与理解.接下来分别从几何光学和波导模式两个角度分析平板波导的各种性质.
几何分析
如下图所示的介质平板波导,其中光沿传播,方向波导厚度无穷大,即仅需要考虑光在方向受约束. 假设,当时称为对称波导.
光在波导内传输需要满足导波条件,即光在平板波导上下界面全放射而束缚在波导内,若不满足全反射条件,光线透过界面往外辐射. 如上图所示沿轴传播的光线视为斜向下和斜向上的平面波,其中沿轴传播常数分别为:
考虑为常数的截面,光在方向被束缚,即此时光在和的两个界面发生全反射,并发生相长干涉,此时光线经历两次全反射并并回到原始位置的相移为,即:
这里为光在界面发生全反射时的相移.上式称为平板波导模式本征方程,即对特定的,存在解.上式也能表示为频率与传播常数的关系,也被称为色散方程.
对s光,也就是TE模有:
其中:
对P光,也就是TM模有:
其中全反射条件为,得到:
即导波条件.定义有效折射率,则导波条件表示为.下面两个图给出了平板波导TE模数值计算结果,其中分别对应 以及的结果

TE模色散曲线

TE模色散曲线
可以发现对于对称波导,其基模无戒指条件,而单时基模存在截止条件.所有 的模式均存在截止条件,随着的减少,波导中能传播的模式数减少,直到仅剩下基模.随着的增加,有效折射率趋于.
现在介绍光波导中另外两个重要的参数,波导的归一化频率定义为:
与波导能传播的模式数目相关.以及数值孔径定义为能波导能束缚的光线最大入射角度的正弦值:
数值孔径是波导的重要参数,越大,波导对光的接受能力越强.
波导模式分析
几何分析能给出波导的大部性质,但无法给出波导模场分布,接下来利用Maxwell 方程分析平板波导中传播的模场分布,对于平板波导,可利用时谐 Maxwell方程:
考虑沿轴传播的平面波解:
代入电磁波方程得到
方程被分为两个相互独立的方程组.其中第一个方程组含有 三个分量,且电场且电场沿方向,与传播方向垂直,为TE模.第二组方程含三个分量,磁场方向沿,垂直传播方向,为模.
分别将方程组进行联立得到:
其中. 上述方程适用平面波导的每一层,加上边界条件,即能得到模场分布.
首先对解进行定性分析(TE模),仍然令.
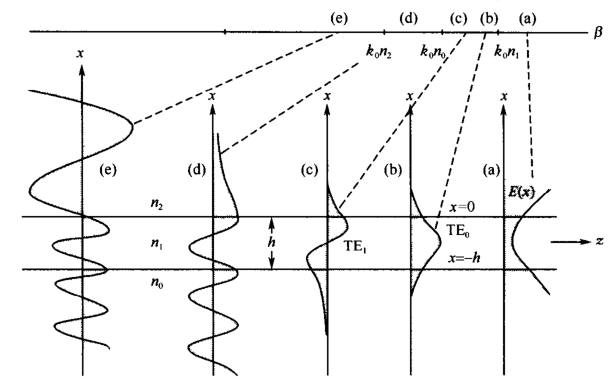
- 若,可知,即在波导的三层都是指数函数,奇恩由于在边界的连续性,最后的场分布随着距离无限增加,这是非物理解.
- 若,波导层,即在波导层为正弦或余弦,形式,而在衬底以及覆盖层都是指数形式,可以找到一个满足边界条件且在衬底和覆盖层都是指数衰减,此时为束缚模.
- ,覆盖层指数衰减,导波层和衬底为振荡函数,成为衬底辐射模.
- ,此时解在三层都是振荡解,称为辐射膜或包层模.
TE模 束缚模满足,在波导的三层分别使用上面的TE模方程,可得到束缚解:
其中
考虑在边界上连续,以及在上连续得到
将用待定常数表示,可将表示为:
考虑在处连续得到:
或写为相位方程得到:
其中与前面定义相同,当然模式本征方程也与几何方法计算结果一样. 利用功率归一化条件,可以确定的值:
其中为波导有效厚度.
TM模场
求解过程与TE模场类似,在边界上,即可得到:
同样有
其中:
对应的相位色散方程:
利用归一化功率,可以得到的取值:
其中TM 模的有效厚度定义为
定义波导归一化参数,归一化频率定义为
归一化传播常数
以及波导非对称参量
若,为对称波导,对极不对称波导.通过归一化参数可将TE模和TM模的模式本征方程写为
通过数值计算,下图给出了归一化折射率随着归一化频率的变化,左图给出了对称波导和非对称波导的模式色散曲线,可以发现对非对称波导存在截止频率.

TE模色散曲线

TE和TM模色散曲线
右图给出了给出时TE模和TM模的色散曲线,其中.
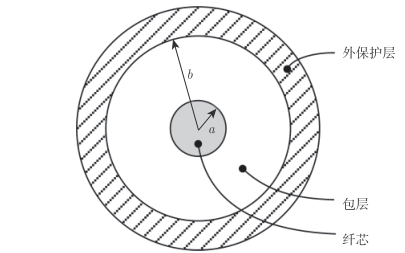
光纤波导
一般的光纤通常由折射率较高的纤芯,折射率较低的包层以及外保护层组成,如下如所示为光纤的截面.
其中光纤截面折射率分布可分为阶跃式和渐变式.下面给出光纤的特征参数:
- 数值孔径:光纤存在接收角,当时,光线才能在光纤中传播,数值孔径定义为,其中.
- 路径色散:光线沿着不同角度会沿着不同的路径传播,从而导致传输时间差.
- 光纤损耗:光纤的损耗包含固有损耗(材料)和外在损耗(缺陷,耦合),通常由单位距离分贝数:损耗大小.
光纤模式分析
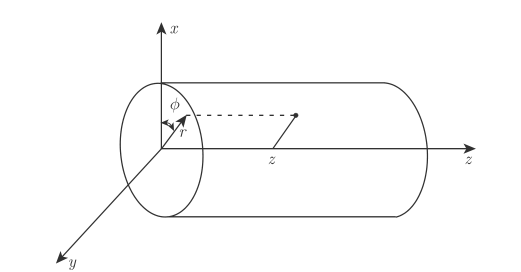
考虑到光纤的对称性,在柱坐标中进行分析,如下图所示:
其中柱坐标中算符形式为:
对于沿轴传播的电磁场,其解可记为:
利用时谐Maxwell 方程,,代入上述解得到:
以及:
利用上述两组微分方程可得到:
其中.可以发现均可由表示,即可被认为是独立分量,且满足标量Helmholtz方程:
上式可用分离变量法求解,以为例,令,代入方程得到
代入方程可得到:
其中第一个方程的解为,第二个方程为贝塞尔方程,其在纤芯和包层的解有所区别,考虑导模存在条件,即对于纤芯,此时方程的解为一阶普通贝塞尔函数,而对包层,此时,,此时贝塞尔方程的解为第二类修正贝赛尔函数.具有物理意义的解因该满足有限,且,此时可忽略解,即可将方程的解记为:
即得到的解:
将解代入前面的方程即可得到以及,详细见, 考虑在边界处连续,可得到:
以及:
即得到了关于系数的方程组,有解的条件为系数矩阵的秩为零,即:
即可得到特征方程为:
这就是光纤导模特征方程,方程中含有三个特征参数,其中只有一个参数独立,对于给定,通过特征方程即能计算出,从而得到模场空间分布.
模式分类
对于给定整数,通常存在多重解,记为,将光纤中模式分为三大类:
- 横向电场(TE模),此时,其中,记为.
- 横向磁场(TM模),此时,其中,记为.
- 混合模式,EH模或HE模.
对模,特征方程简化为
利用上式简化为
由,可得
其他分量为零即.
对TM模,特征方程为
可简化为
由,可得
其它分量为零.
对于一般情形,可考虑弱波导近视,即,此时有近似,且,代入特征方程并对两边开根号即得到
其中,取正号时利用贝塞尔函数特性,得到EH模
取负号时得到HE模
通过数值求解的方法可对本征方程求解,从而得到本征解,每个对应一个可能的模式,记为(以为主),(以为主).
定性分析
将TE模和TM做简并模处理,满足共同的特征方程,即
其中,且,为归一化频率,即可将方程两边都写为关于的函数,即,可将函数在同一个图中表示,函数的交点即特征方程的解,如下图所示
令为的第个零点,可以发现对于不同的,函数的交点个数不同,若,则两个函数有个交点,即特征方程有个解,且第特征方程第个解满足. 特别是当时函数将不存在交点,即不存导模,,称为截止频率.当时,此时方程有三个解,即存在个TE模式和个TM模式.
对模,可令,将函数在同一图中画出,如下图所示()
若,此时曲线将会有个零点,特征方程的第个根满足. EH 模的最低解模为,其截止频率,当时光纤中不存在EH导模.
对模,当时,,如下图所示:
曲线的第个交点满足,由于,因此任有意义.此时最低阶模,其截止频率,也就是模不截止,也被称为光纤主模.
当,此时,将函数在同一图中画出,如下图所示
考虑到,因此曲线的交点一定在的解和之间,其中可化简为,即得解,也就是说特征方程的第个根满足.的截止限为,最低阶模式的截止频率.
除了的TE和TM模式,每个混合模都是双重简并,这是由于其角向场可选择两个相互独立的函数.
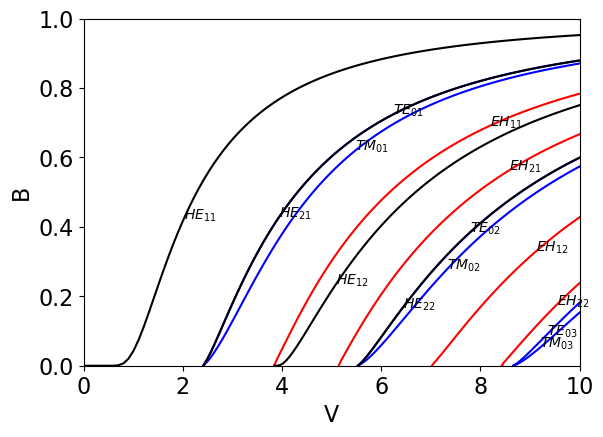
模式色散曲线
与前面类似,引入特征参数归一化频率,以及归一化的传播常数,可知满足,则可将各个模式特征方程都记为特定归一化频率下关于的方程,一旦确定即可可确定导模,下图给出了归一化的模式色散曲线
可以发现当时,仅存在导模. 另一个需要注意的时除了外,其它所有模式均为双重简并.
线偏振(LP)模
考虑电场横场和纵场的振幅之比,磁场也有同样的关系,表明方向上的分量非常小,即弱导光纤可以做TEM 波处理,此时电场和磁场均与传播方向垂直,且传播过程中偏振状态不变,称为线偏振(LP)模.
对与LP模式,近似认为横向电场和磁场满足标量Helmoholtz方程,若令横向电场的方向沿轴,其满足的Hemholtz方程为
求解过程与前面类似,可得到:
利用上式即可得到:
得到
同样的方法可以得到,不再赘述.考虑和在边界处连续,可得到:
即得到关于的齐方程,上式有解的条件为系数矩阵的秩为零,得到:
得到本征方程
其中,利用贝塞尔函数递推关系:
可得
或
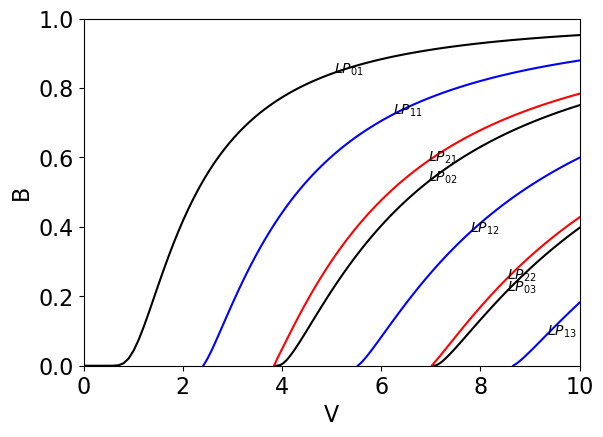
上述公式即模式的特征方程,与矢量模式相比要简单许多.下面给出线偏振模式的色散曲线,其中参数定义与前面相同:
可以发现当时,只能存在一个导模,这与矢量模分析结果一样. 由于线偏模分为和两组,即存在两个不同偏振导模,且对于,有和两种可能性,因此当时,每一个LP模式四重简并.
下面的表格给出了线偏振模式与矢量模的简并关系
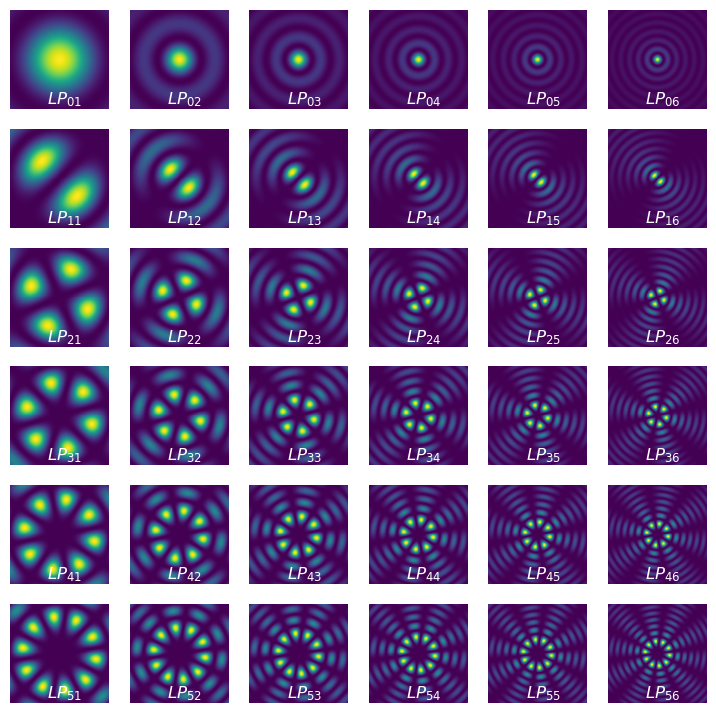
下图给出了不同线偏振模式截面场强分布